数をかぞえられない学生たち ありもしない「公式」に頼り…算数教育の珍現象
1月下旬から3月上旬にかけて中学・高校・大学の入学試験シーズンである。中学入試の算数から大学入試の数学に至るまで、学生たちがとくに共通して苦手とする内容がある。それは「数をかぞえる問題」だ。桜美林大学の芳沢光雄教授が解説する。
＊＊＊
速報「娘はフェイク情報を信じて拒食症で死んだ」「同級生が違法薬物にハマり行方不明に」 豪「SNS禁止法」の深刻過ぎる背景
速報「ウンチでも食ってろ！と写真を添付し…」 兵庫県知事選、斎藤元彦氏の対抗馬らが受けた暴言、いやがらせの数々
筆者は複数の大学に専任教員として42年間勤務し、入学試験に関しては数学責任者を含めて深く関わってきた。また、文系・理系の大学生約1万5千人に対する授業、および全国各地の小中高校でのべ1万5千人に対する出前授業を経験し、また筆者のゼミナール出身の多くの教員から現場の状況を伝えられている。
本稿ではそれらの経験も踏まえて、「数をかぞえる問題」が出題されると成績が極端に悪くなることの原因、さらには「数をかぞえること」が今後のAI時代にとって本質的に重要であることを指摘する。
そもそも人類は、物事を「かぞえる」ことを始めて、発展してきたといえる。歴史を振り返ると紀元前8000年頃から始まる新石器時代の近東には、小さな粘土製品の「トークン」というものがあった。壺に入った油は卵型のトークンで数え、小単位の穀物は円錐形のトークンでかぞえる、というように物品それぞれに応じた特定のトークンがあった。1壺の油は卵型トークン1個で、2壺の油は卵型トークン2個で、3壺の油は卵型トークン3個でというように、1つ1つに対応させる関係に基づいて使われていた。
その後、個々の物品の概念から独立して整数の概念が誕生したのであるが、これこそが人類が大きく発展した本質であろう。「数」によって客観的な議論ができるようになったからである。1950年にノーベル文学賞を受賞したバートランド・ラッセルは、「ひとつがいの雉（きじ）も2日も、ともに2という数の実例であることを発見するには長い年月を要したのである」という言葉を遺している。
誰でも幼少の頃には、イチ、ニ、サン、シ、……と素朴にかぞえることを教えられただろう。しかし、高校入試の中学生、大学入試の高校生、就職適性検査を受ける大学生がなぜ「数をかぞえる問題」を苦手とするのかを探ると、人類にとって極めて大切な「素朴にかぞえること」は忘れ、「数をかぞえる方法」の暗記から算数・数学の学びを始めていることが分かる。
数をかぞえる問題に関して、少し考えて分からないとなると、「この問題の解き方を教えてください」、「この問題はどのような公式を使って解くのですか」という質問が次々と寄せられるのである。そのような質問をする生徒や学生に出会う度に、「この方々は、幼少の頃に素朴にかぞえる教育を受けていたのだろうか」と疑問に思ってしまう。
さらに、高校入試、大学入試、就職適性検査、それぞれの参考書を見ても、素朴にかぞえることの意義については言及されていない。最初から順列や組合せの個数をかぞえるときに使う方法、とくに順列記号Pや組合せ記号Cに関する公式を覚えさせる指導から入っている。さらに、なんでもPやCを使わないといけないという強迫観念のようなものを植え付けているようにさえ感じることもある。
ちなみに順列とは、たとえば7人から3人を選んで1番、2番、3番と並べる場合にどんな並べ方があるかの総数のようなものである。また組み合わせとは、たとえば7人から単に3人を選ぶ場合の総数のようなものである。筆者が訴えたいことは、公式に当てはめて計算するような、この種の問題に関することではなく、素朴にかぞえる問題に関することである。
小学生でも解くことが可能な以下のような問題1～3で、無理にPやCの公式を使って解こうとしたり、解答を得るための（ありもしない）“公式”を尋ねたりするような、珍現象を次々と起こしている大学生（高校生）がいることを訴えたいのである。しかも、微分を用いて極大値や極小値を求めることができる真面目な大学生にも、そのような者がいることに注目したい。中にはPやCを使った理解不能な式を書いて、桁外れの大きい数を「答え」として書いて平然としている者もいる。
なお、正解を得る・得ないは二の次のことであり、いろいろ試行錯誤しながらじっくり考えることが大切であると言いたい。
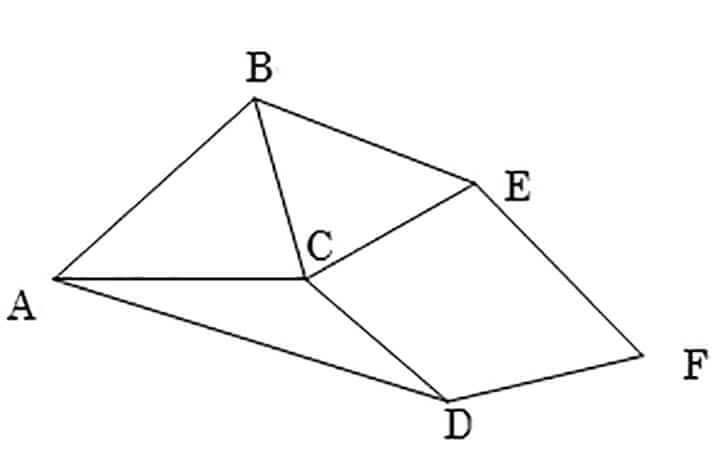
問題1 図Aのような路線図があるとき、出発地Aから到着地Fに至るルートは何本あるだろうか。ただし、同じ地点は2度通らないものとする。
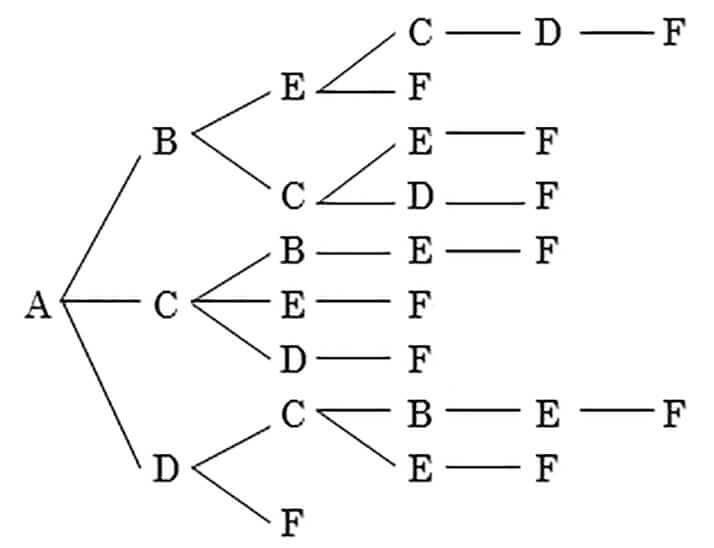
これは、図Bのように樹形図を用いてすべてのルートを列挙すると、求めるルートは10本であることが分かる。
問題2 同じ形の白と黒の玉を合計5個使って、ネックレスを作りたい。何通りのネックレスが考えられるだろうか。なお、全部白でも全部黒でも構わない。また、ネックレスは表と裏がないことにも注意する。
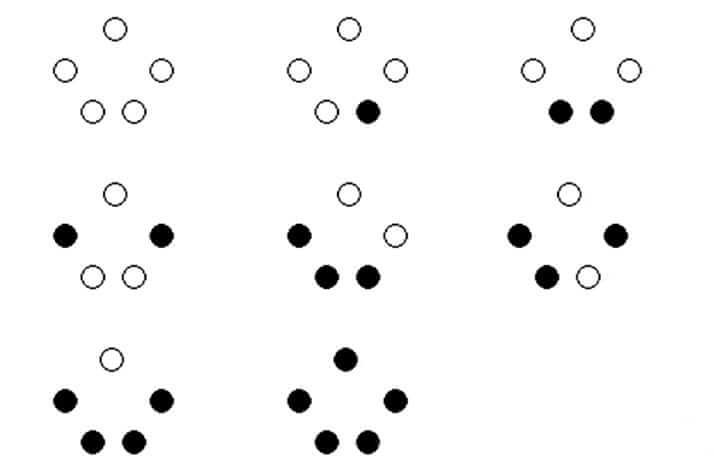
対称性を利用して具体的に調べることにより、以下の8通りのネックレスが考えられる（図Cも参照）。
全部が白・・・1通り
1個が黒・・・1通り
2個が黒・・・2通り
3個が黒・・・2通り
4個が黒・・・1通り
全部が黒・・・1通り
問題3（就活適性検査レベルの問題） アルバイト店員が何人か在籍する年中無休のお店で、次の形態で一週間のスケジュールを組むとする。
（ⅰ）アルバイト店員は、誰もが1週間にちょうど3日出勤する。
（ⅱ）何曜日でも、ちょうど30名のアルバイト店員が出勤する。
以上の条件のもとで、アルバイト店員の総人数は何人になるだろうか。（ヒント：（ⅰ）と（ⅱ）それぞれから、1週間の延べアルバイト人数をかぞえてみる。）
いまアルバイト店員の総人数を△とすると、（ⅰ）より1週間の延べアルバイト人数は3×△である。一方で（ⅱ）より、この人数は30×7である。したがって、
3×△＝30×7
から△＝70（人）が分かる。
次の問題は2007年度の京都大学入学試験問題で、「算数で解ける大学入試問題」として話題にもなった。
問題4 1歩で1段または2段のいずれかで階段を昇るとき、1歩で2段昇ることは連続しないものとする。15段の階段を昇る昇り方は何通りあるかを求めよ。（答えは277）。
かなり難しい問題ではあるが、3段目まで昇るには何通りあるか、4段目まで昇るには何通りあるか、5段目まで昇るには何通りあるか、というように数えていくことにより、規則性が分かって正解に至る問題である。もちろん、解ける必要はない問題であるが、「数をかぞえること」の意義を世間に浸透させた点で高く評価したいものである。（参考までに、3段目まで昇るのは、［1段→1段→1段］、［2段→1段］、［1段→2段］の3通りである。）
ところで、数学には「離散数学」という分野がある。これは主に、微分積分とは無縁な有限個の世界を対象として、とくにAI時代に重要な符号理論やアルゴリズム論などの基礎になる。また、高校の学習指導要領にも含めることが検討されたこともある。研究手法としては、「対称性を利用してかぞえる」（問題2参照）、「2通りにかぞえる」（問題3参照）、「帰納的にかぞえる」（問題4参照）などの「かぞえること」が特徴としてある。
そのような背景を踏まえて昨年末に、筆者は高校生でも一歩ずつ読むことが可能な『離散数学入門～整数の誕生から「無限」まで』（講談社ブルーバックス）を出版した（問題4の解説も掲載）。趣旨は、きちんとかぞえることの上に「離散数学」が成り立っていることである。
[1/2ページ]
