算数教育の危機 「2億円は50億円の何%？」大学生の2割が間違えるという現実
日本でもようやく来年2020年度から、小学校でプログラミング教育が導入される運びとなった。その背景にはIT分野の人材育成が諸外国に比べて、明らかに遅れていて、将来のAI時代を迎えるにあたり、危機感が高まっているという実態がある。桜美林大学の芳沢光雄教授が解説する。
＊＊＊
速報「パンに虫が」「変な味がする」 山崎製パン元社員が重大証言、クレーム対応の“マル秘テクニック”は「客を装っての“ダマでの買い取り”」
速報ウエルシア社長の電撃辞任、原因は中国人女性との不倫だった 女性は取引先の関係者
インドなどのIT教育が進んでいる国々と比べて、上記の主張を展開する記事をよく見かける。しかし、インドと日本では置かれている状況がまったく異なっている。それは一言で言ってしまえば、子どもへの算数教育だ。
日本とインドの算数教育を比較すると、インドは日本よりも学年、地域、私立学校などにより違いがあるとはいえ、授業時間数が約1.5倍とはるかに多く、さらに「理解」を大切にする教育を実践している。日本はその部分が大きく欠落しているのだ。
しかも、日本の場合、インドや中国の1割ほどの人口なので、本当はこれらの国の上位のクラス並に算数教育を充実させなければ、国際社会に勝っていくことは難しいにもかかわらずだ。
ゆとり教育時代の教科書は時代に逆行
今でこそ見直されてきた「ゆとり教育」だが、算数・数学教育の「理解」の面で形骸化した実態を紹介しよう。
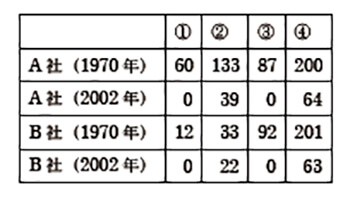
【図1】は2013年度の筆者のゼミナール生が、教科書研究センターで調査して得たものである。（1）小数・分数の混合計算（小学校教科書）、（2）3つ以上の数字が入った四則混合計算（小学校教科書）、（3）3桁×2桁以上の掛け算（小学校教科書）、（4）全文記述の証明問題（中学校教科書）は、算数・数学教科書でシェアの大きいA社、B社の教科書に掲載されている問題数の年別比較である。
（1）に関しては、混合計算、つまり数字を小数か分数のどちらかに統一しなければ計算ができないという問題だが、ゆとり教育時代はその問題がまったく扱われなくなっていたのである。当然、インドの教科書にはこの類の問題は相当多くある。ちなみに計算機でこれらの計算を行なう場合、一般に前者は実数計算で後者は整数計算となり、データの扱いが異なる。
（2）の3つ以上の四則混合計算問題に関しても減少傾向が見られる。これによって、学校では計算の順序をまともに教えなくなったため、足し算、引き算、かけ算、割り算が交ざっていると、満足に計算できないという日本人も多くなったのだ。
日本では2006年7月に国立教育政策研究所が発表した「特定の課題に関する調査（算数・数学）」（小学4年生から中学3年生までの約3万7千人対象）には、「3＋2×4」の正解率が、小4、小5、小6と学年が上がるにしたがって、73.6%、66.0%、58.1%と逆に下がっていくとのデータがあった。この計算規則は、計算機で演算の順序を規定するために本質的に重要である。
インドの教科書では、「計算規則を設けないとバラバラの答えが出てしまう」ことを最初に示し、掛け算や割り算は、足し算や引き算よりも先に計算するなどの規則をしっかり教えてから多くの問題を行なう。
（3）の3桁×2桁以上の掛け算問題は、ゆとり教育当時の教科書への記載は皆無だ。「ゆとり教育」では、「2桁同士の掛け算ができれば、3桁同士の掛け算などもできる」という無責任な考え方によって、諸外国や過去の日本の教育に例を見ない、2桁同士の掛け算の教育だけで終らせてしまった。
筆者は以前から、3桁同士の掛け算をきちんと教えるよう主張してきたが、それには深い理由がある。その意義を説明しよう。
まず2桁や3桁のかけ算は「ドミノ倒し」に例えられる。「ドミノの牌」はかける数やかけられる数を表す。2つだけの牌では、倒すと倒されるだけの関係である。
【図2】の2桁同士のかけ算では、最初に8×9＝72を行ない、その十の位の7を、次の計算5×9＝45に加える。ここで、「7を渡すこと」と「7をもらって加えること」は、2つのドミノの「倒すもの」と「倒されるもの」に相当する。
しかし、3つの牌になると、根本的な計算構造が変わる。どういうことかというと、最初に7×9＝63を行ない、その十の位の6を、次に行なう4×9＝36に加えて42となり、さらにその百の位の4を、次に行なう7×9＝63に加える。つまり、4×9のところでは「6をもらって加えること」と、「4を渡すこと」の2つの作業をしていることを指し、3個のドミノ倒しで「倒されると同時に倒す真ん中の牌」に相当するのだ。
2桁同士のかけ算では、下から繰り上がってきた数を受け取りつつ、上の位に数を渡すという仕組みを学ぶことができない。だから、3桁以上のかけ算を、子どもたちは戸惑うのがゆとり教育時代の算数教育の状況だ。
前出の国立教育政策研究所が発表した調査結果では、小学4年生を対象とした「21×32」の正答率が82.0%であったものの、「12×231」のそれは51.1%に急落。小学5年生を対象とした「3.8×2.4」の正答率が84.0%であったものの、「2.43×5.6」だと55.9%に急落した。
4桁以上の掛け算では、新たな作業が加わることなく次々と続いていくことが分かる。だからこそ、3桁同士の掛け算は重要で、インドの教科書では丁寧に説明した後に多くの問題を課している。ちなみに、次々と続いていく作業は計算機ではよく行うので、掛け算の仕組みでしっかり学んでおくとよい。
（4）の全文記述の問題の掲載数も著しく減少した。論証教育を重視するインドの教科書では、多くの記述問題が掲載されている。また、計算機のプログラム文を書くことと数学の証明文を書くことは、水も漏らさぬように論理を積み重ねていく点で似ている。
学力の国際調査結果で日本に関してよく指摘されることは、「いわゆる単純な計算は得意であるが、説明文の答案には白紙が多い」ことである。
2004年2月に行われた千葉県の県立高校入試の国語では、地図を見ながら「おじいちゃん」に道案内することを想定した文を書く問題が出題されたが、結果はなんと受験者の半数が0点だったのだ。地図の説明は、筋道を立てて論理的に説明する力を見る点で適当な題材であり、中学数学における図形の作図文や証明文の学びをいかに大切にすべきか、を示している。
筆者は、文部科学省委嘱事業の「（算数）教科書の改善・充実に関する研究事業」専門家会議委員に任命され（2006年11月～2008年3月）、上記の持論を最終答申に盛り込んでいただいた。その後の算数教科書は改善されてきている。
「%」を理解していない大学生
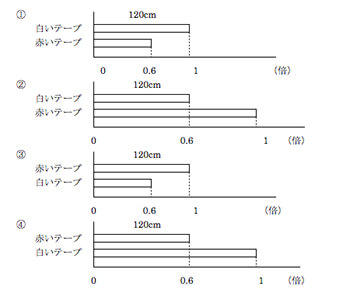
ところが、それでもなお、取り組みの成果がまったく見えない分野がある。割合の「%」の分野だ。2012年の全国学力テスト（小学6年算数）で、「赤いテープの長さは120 cm、赤いテープの長さは白いテープの長さの0.6倍」ということが分かっているという前提で、その意味を示す図を（1）から（4）の4つから選択させる問題が出題された（【図3】）。誤解答の（3）を回答した生徒が50.9%もいる半面、正解の（4）を回答した生徒が34.3%しかいなかったのである。
また、2012年度の全国学力テストから加わった理科の中学分野（中学3年対象）では、「10%の食塩水を千グラムつくるのに必要な食塩と水の質量」を求めさせる問題が出題された。が、「食塩100グラム」「水900グラム」と正しく答えられた生徒は52.0%に過ぎなかった。1983年に、同じ中学3年を対象にした全国規模の学力テストでもほぼ同一の問題が出題されたが、この時の正解率は69.8%だったのである。
上記2つの問題の結果から、「元にする量」と「比べられる量」の理解が不十分なまま進学していくことが分かる。それらの用語の意味を理解せずに、「く（比べられる量）・も（元にする量）・わ（割合）」という公式を覚えて当てはめる「やり方」だけの暗記教育が学校教育でも流行っていることが主な原因だと考えられる。つまり、「元にする量」と「比べられる量」を取り違えても気付かないのである。
そのままの状態で大学へ入学する者も多く、いわゆる有名私立大学文系学部に在籍する学生でも「%」を理解していない者は少なくない。この10年間に、「%」に関して他大学の関係者から、何件もの困惑する話が寄せられており、そのなかには「多項式に関する微分・積分の計算はできるものの、%を理解していない学生がいる」という証言がいくつかある。
いろいろな調査から「2億円は50億円の何%か」という質問では2割ぐらいの大学生が間違え、50を2で割って「25%」という誤答が目立つ。もちろん正解は、2を50で割って（100を掛けて）「4%」となる。
さらに、「西暦2000年に対し2001年は10%成長し、西暦2001年に対し2002年は20%成長したもの（売上高など）は、西暦2000年に対し2002年は何%成長したことになるか」という質問では、10に20を加えて「30%」とする誤答が正解より目立つ。ちなみに正解は、1.1×1.2と計算して、結果の1.32から「32%」である。
プログラミング教育の前に算数教育の充実を！
21世紀になってしばらく経った頃、松井証券の松井道夫社長は、「21世紀の時代は20世紀までの合計量の評価ではなく、単位当たりの評価になってきた」という内容を述べられた。これは、20世紀までの「＋（足し算）」から「%」の時代になったことを意味している。たとえばGDPに関しても、1人当たりのGDPという見方がよく使われるようになってきている。
それだけに、ITでプログラムを作成するときなど、重要な単語である「%」に関する取り扱いで、間違いなどあってはならない。
昭和の「いざなぎ景気」超えを果たした2006年11月頃には、新聞やテレビ報道などがこぞって誤った数字を報じた。平成の景気と対比する形で「いざなぎ景気」の年平均成長率を取り上げたわけだが「14.3%」と報じる媒体があれば「11.5%」と紹介するものもあった。これは、相乗平均の考え方で算出した11.5%が正しく、相加平均の考え方で算出した14.3%は間違いであることを、拙著などで何回か指摘したことを思い出す。
このような注意点もあるだけに、「%」の扱いは軽んじてはならないのだ。
上で述べてきたように、「教育の犠牲者」とも言える若者を育ててしまった「やり方」暗記の教育から、「理解」重視の教育へ、日本の教育が速やかに、かつ大胆に舵を切らなくては手遅れになるだろう。
最近の新聞各紙では、来たるAI時代を視野に置いて、小学校におけるプログラミング教育に関して積極的に言及している。しかし、その基礎である算数教育の本質的な部分にある深刻な問題点には、「プログラミングと算数は別」という立場から無視を決め込んでいる。
また一部のIT企業の関係者は、「IT企業で難しい微分・積分を使うのはほんの一部であり、多くは算数の四則計算で済む内容なので、数学が苦手な方が入社されても困りません」という発言を積極的にしている。ある点でこの発言は正しいのかもしれないが、算数を正しく「理解」していない人間に、プログラムの作成を任せられるだろうか。
「やり方」暗記教育が改善されない背景には、プロセスがメチャメチャでも答えだけを当てればOKという「マークシート式問題」の影響もある。国もようやくその問題点に気付いて、一部記述式の大学入試共通テストを導入する運びとなった。
筆者は本年4月に『「%」が分からない大学生～日本の数学教育の致命的欠陥』（光文社新書）を出版し、7月上旬には『AI時代を切りひらく算数～「理解」と「応用」を大切にする6年間の学び』（日本評論社）という教育書をつづけて出版した。
日本の算数教育が、「やり方」だけ暗記させる誤魔化しの教育から、「根本」を理解させるプロセス重視の教育に変わることを祈りつつ、これからも引き続き、精進していきたい所存である。
